A Deceptively Difficult Problem
- Vishnu Vusirikala
- Aug 9, 2021
- 3 min read
What you can miss a question

Hey guys! Recently, I received a question from my friend that I thought I should share with you all:
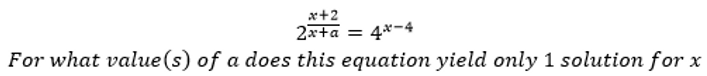
Quite a simple question on the face of it. When he gave this to me, my immediate response was a=2 as the exponent of 2 would cancel out giving only 1 solution for x. However, his immediate response was, “How?” I then showed him this working:

This seemed to be correct but he wanted me to do the longer method without substituting a random value of a. So I did, and this is what I got:

Over here, as the discriminant is lesser than 0, a has no real roots! However, we just showed that a=2 was a solution for a that gave only 1 solution for x i.e. 9/2. This stumped both of us. Pondering on this, I tried to prove that a=2 gives more than 1 solution for x. This is what I did:
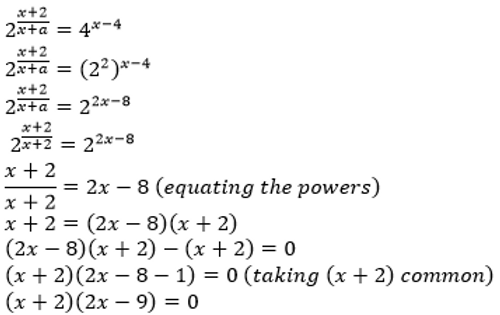
Notice over here that we got 2 equations in terms of x at a=2: x+2=0 and 2x-9=0. However, and this is the main reason why we didn’t get a solution before, x+2 cannot be equal to 0. This is because the exponent for 2 in the question, which has x+a in the denominator, cannot have x+a equal to 0 as we cannot divide anything by 0! As we take a=2, x+2 now cannot be 0. Therefore, x+2=0 is an invalid equation and x=9/2 is the only solution. In the long method, we are just finding the values of a which yield 1 solution for x without any restrictions. Now this leads us to a new question, how do we solve this question then without random substitution?
After using the long method, we see that there are no solutions for x. But now we have a restriction that x-a cannot be equal to 0. Again from the long method, we see that we obtain a quadratic in x with a in some of the terms i.e. 2x²+x(2a-9)-(8a+2). By using the method that we used, we get to know that the quadratic will never break up into a square as it is impossible to obtain only 1 solution for x. As it turns out, the quadratic is not perfectly factorizable and can only be expressed in the form (nx+y)(mx+z)+R(a). This is how the quadratic is broken down, but to get a solution for the question we need to assume that x+a is a factor of the quadratic. So, we can rewrite it again as (x+a)(mx+z)+R(a), where R(a) is equal to 0. With this weapon in our hand, we can solve this question in 2 different ways.
Method 1:
As we know that one of the factors is x+a to get a single solution for x, substituting x=-a in the quadratic has to yield 0. With this, we can solve for a:
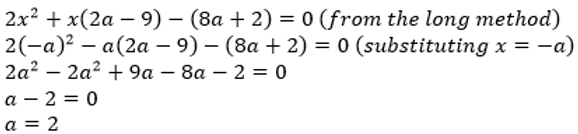
This only gives us our correct solution of a=2.
You can also notice over here that a-2 is actually the remainder, R(a), that we obtain when we divide the quadratic by x+a. This is because from the simplified form i.e. (x+a)(mx+z)+R(a), if we substitute x=-a into this, we will only be left with the remainder as x+a will be equal to 0 at x=-a. This shows that the R(a) is equal to a-2. We actually get this from the remainder theorem: P(-b/a), here P(-a), is the remainder when ax+b, here x+a, is the divisor. The importance of this will be elaborated in the next method.
Method 2:
Note: I have written an article on synthetic division and you can view it here.
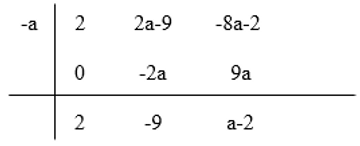
Here, we see that the remainder is a-2. From the synthetic division, we can rewrite the quadratic as (x+a)(2x-9)+a-2. This is a simplified version of the equation (x+a)(mx+z)+R(a), where m=2, z=-9 and R(a)=a-2. As x+a is a factor, R(a) has to be equal to 0. So, a-2 should be equal to 0. This finally gives us a=2, which is what we had got previously. If we substitute this value of a into the equation above, we will get (x+2)(2x-9). This also correctly shows the factorized quadratic we were supposed to receive.
That gives us the final solution for this question as a=2. Although simply looking at the question can give you this value, you now know how to actually obtain this value. That simple question turned out to be quite worth the trouble don’t you think?






Comments